CODIGOS BINARIOS, TRANSFORMACIONES DE BINARIO A DECIMAL Y VICEVERSA
CÓDIGOS BINARIOS:
El código binario es el sistema numérico usado para la
representación de textos, o procesadores de instrucciones de computadora, utilizando el sistema binario(sistema numérico de
dos dígitos, o bit:
el "0" /cerrado/ y el "1" /abierto/). En informática y telecomunicaciones, el código binario
se utiliza con variados métodos de codificación de datos, tales como cadenas de
caracteres, o cadenas de bits. Estos métodos pueden ser de ancho fijo o ancho
variable. Por ejemplo en el caso de un CD, las señales que reflejarán el
"láser" que rebotará en el CD y será recepcionado por un sensor de distinta
forma indicando así, si es un cero o un uno.
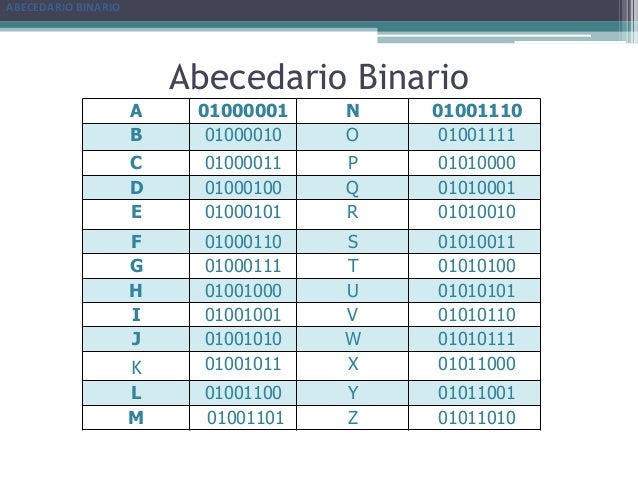
En un código binario de ancho fijo, cada
letra, dígito, u otros símbolos, están representados por una cadena de bits de
la misma longitud, como un número binario que, por lo general, aparece en las
tablas en notación octal, decimal o hexadecimal
Según Anton Glaser, en su History of Binary and other Nondecimal
Numeration, comenta que los primeros códigos binarios se utilizaron en
el año 1932: C.E. Wynn-Williams ("Scale of Two"), posteriormente en
1938: Atanasoff-Berry Computer,
y en 1939: Stibitz ("excess three") el código en Complex Computer.
Es frecuente también ver la palabra bit referida bien a la ausencia
de señal, expresada con el dígito "0", o bien referida a la
existencia de la misma, expresada con el dígito "1". El byte es un
grupo de 8 bits, es decir en él tenemos 256 posibles estados binarios.
El código binario es el sistema numérico usado para la representación de textos, o procesadores de instrucciones de computadora, utilizando el sistema binario(sistema numérico de dos dígitos, o bit: el "0" /cerrado/ y el "1" /abierto/). En informática y telecomunicaciones, el código binario se utiliza con variados métodos de codificación de datos, tales como cadenas de caracteres, o cadenas de bits. Estos métodos pueden ser de ancho fijo o ancho variable. Por ejemplo en el caso de un CD, las señales que reflejarán el "láser" que rebotará en el CD y será recepcionado por un sensor de distinta forma indicando así, si es un cero o un uno.
Según Anton Glaser, en su History of Binary and other Nondecimal
Numeration, comenta que los primeros códigos binarios se utilizaron en
el año 1932: C.E. Wynn-Williams ("Scale of Two"), posteriormente en
1938: Atanasoff-Berry Computer,
y en 1939: Stibitz ("excess three") el código en Complex Computer.
TRANSFORMACIONES DE BINARIO A DECIMAL Y VICEVERSA
BINARIO Y DECIMAL: En el Sistema Decimal podemos escribir números como 451, 672, 30, etc. Es decir, podemos formar cualquier combinación de los dígitos del 0 al 9 (cifras).
En Sistema Binario podemos escribir números como 01100111, 1110, 011, 1, etc.
Es decir, podemos formar cualquier combinación de los dígitos 0 y 1 (bits). Cada número en Sistema Decimal tiene su equivalente en Sistema Binario, y viceversa. Pero…¿Cómo se convierten los números de Sistema Binario a Sistema Decimal?
Observa el siguiente ejemplo:
Vamos a convertir el número 11001011 a Sistema decimal:
PASO 1 – Numeramos los bits de derecha a izquierda comenzando desde el 0.
PASO 2 – A cada bit le hacemos corresponder una potencia de base 2 y exponente igual al número de bit.
PASO 3 – Por último se suman todas las potencias. 7 6 5 4 3 2 1 0 exponentes 1 . 2 7 + 1 . 2 6 + 0 . 2 5 + 0 . 2 4 + 1 . 23 + 0 . 22 + 1 . 21 + 1 . 20 = 128 + 64 + 8 + 2 + 1 =203
Y….¿Cómo se convierten los números de Sistema Decimal a Sistema Binario?
Observa el siguiente ejemplo y contesta a los ejercicios que se te proponen a continuación. Vamos a convertir el número 45 a Sistema Binario:
PASO 1 – Dividimos 45 entre 2 sucesivamente, sin sacar decimales, hasta obtener un cociente igual a 1.
PASO 2 – Leemos el último cociente y todos los restos en sentido contrario a cómo han ido apareciendo.
PASO 3 – En caso de que nos pidan el resultado dentro de un byte rellenamos con ceros por delante hasta completar los ocho bits.
Comentarios
Publicar un comentario